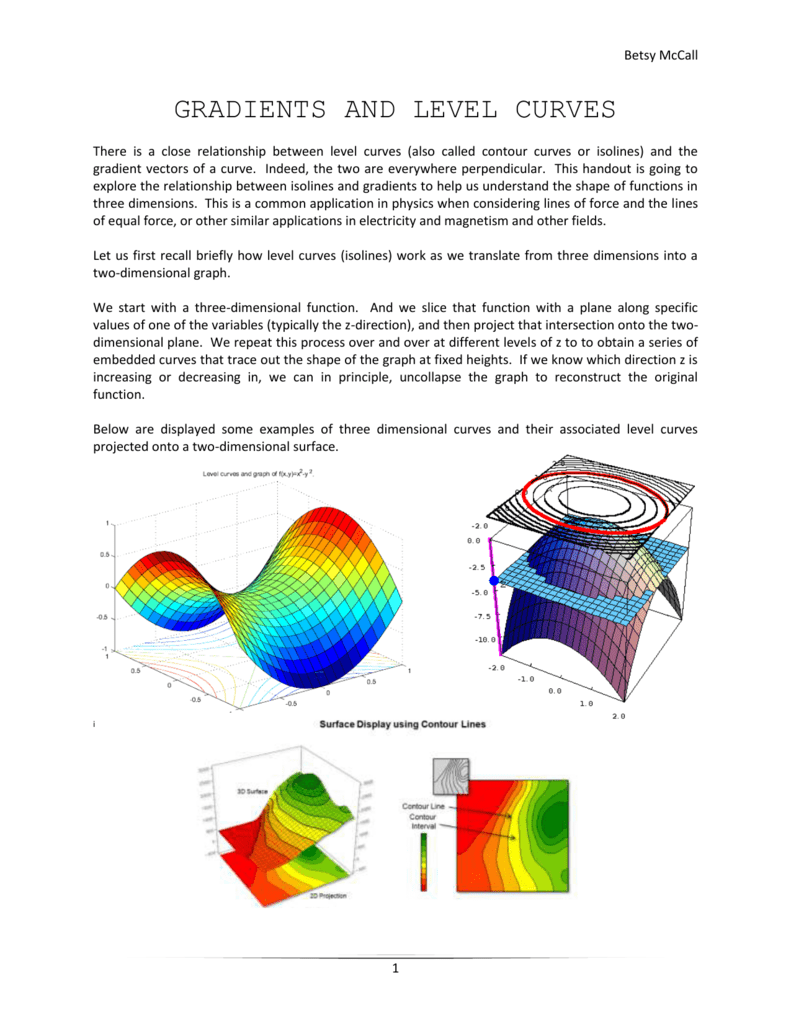
Level curves MIT 1802SC Multivariable Calculus, Fall 10Abstract In this chapter we discuss the problems and theorems of the previous chapter using some new terminology The concepts we are going to examine here revolve around functions defined on a plane and their level curvesThese are especially useful in the solutions to problems involving maxima and minimaThe Gradient and the Level Curve Our text does not show this, but the fact that the gradient is orthogonal to the level curve comes up again and again, and in fact, the text proves a more complicated version in three dimensions (the gradient is orthogonal to the level surface) It is important, so we go through a proof and an example

16 1 Functions Of Several Variables
Level curves and level surfaces
Level curves and level surfaces-When the number of independent variables is two, a level set is called a level curve, also known as contour line or isoline;AutoCAD Map 3D Forum Welcome to Autodesk's AutoCAD Map 3D Forums Share your knowledge, ask questions, and explore popular AutoCAD Map 3D topics cancel Turn on suggestions Autosuggest helps you quickly narrow down your search



Problem On Surfaces And Level Curves Leading Lesson
Level Curves and Contour Plots Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant高数 level curve 怎么理解? 关注者 2 被浏览 777 1 个回答 胡宇铭 3 人 赞同了该回答 我直接把我学校的教材截图给你吧,是英文的,觉得说得很清楚明了了。 The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)
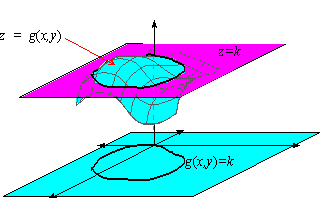
Sketch some level curves of the function Solution First, let z be equal to k, to get f(x,y) = k Secondly, we get the level curves, or Notice that for k>0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves of f(x,y)Remark 1 Level curves of a function of two variables can be drawn in an ( x, y) coordinate system;A level curve of a function $f(x,y)$ is the curve of points $(x,y)$ where $f(x,y)$ is some constant value A level curve is simply a cross section of the graph of $z=f(x,y)$ taken at a constant value, say $z=c$ A function has many level curves, as one obtains a different level curve for each value of $c$ in the range of $f(x,y)$
Level Curve A level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14) SEE ALSO Contour Plot, Equipotential Curve, Level Surface, Phase Curve REFERENCES Tabor, M Chaos and Integrability in Nonlinear Dynamics An Introduction New York Wiley, 19Level Curves of a Paraboloid This example requires WebGL Visit getwebglorg for more info When we lift the level curves up onto the graph, we get "horizontal traces" This will give us the sketch of level curves of the function In this video we're going to talk about how to find the level curves both graphically (by looking at a picture of the threedimensional figure) and algebraically, by replacing z in the multivariable function with a constant c, and then substituting different values for c in order to




Math 15 Lecture 7 Level Curves And Contour Plots Oneclass




Problems With Level Curves First Steps Julialang
So a level curve is the set of all realvalued solutions of an equation in two variables x 1 and x 2The Kuznets curve (/ ˈ k ʌ z n ɛ t s /) expresses a hypothesis advanced by economist Simon Kuznets in the 1950s and 1960s According to this hypothesis, as an economy develops, market forces first increase and then decrease economic inequalityThe Kuznets curve appeared to be consistent with experience at the time it was proposed However, since the 1960s, inequality has risen in the USGradients and Level Curves The gradient of a function is a vector field over the domain of the function We can see what the above vector field looks like First we need to load an external package for plotting vector fields Type the following command exactly (notice that the single quotes are single left quotes), Needs "Graphics`PlotField`"



Level Curves Project Project




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
No headers Recall that the level curves of a function f ( x, y) are the curves given by f ( x, y) = constant Recall also that the gradient ∇ f is orthogonal to the level curves of f Back to top 34 Grad, curl and div 36 Line Integrals I have never used matlab before and have no idea how to plot level curves I looked online and most results involve using contour but not exactly sure how to specify the upper limit of z 0 Comments Show Hide 1 older comments Sign in to comment Sign in to answer this questionThe increment \ (\Delta t\) for the level curves to plot, defaults to 10percent intervals If delt=05, then only the median plus the consequences of a defined getlevel is used



S0 3



Problem On Surfaces And Level Curves Leading Lesson
Traces, level curves, and contuour maps Click here for a printable pdf version TRACES The trace of a surface in a plane is the intersection of the surface with that plane While we can discuss traces in any plane, for surfaces in the form z = f(x,y) we are particularly interested in traces in planes parallel to the xy planeIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionAt Level The Curve, we aim to make everyday life easier for people by creating products that adapt to the customers' needs and wants, and at a low price The result is a consumeroriented approach which caters specifically to, as our name suggests, "leveling the curve" as well as the "playing field" for the disabled community



Gradients Level Curves




16 1 Functions Of Several Variables
The level curves of f(x,y) are curves in the xyplane along which f has a constant value A level curve of a function f(x,y) is a set of points (x,y) in the plane such that f(x,y)=c for a fixed value c Example 5 The level curves of f(x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of cLEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Draw Level Curves For Functions Of Two Variables In C C Helper
Kontrollera 'level curve' översättningar till svenska Titta igenom exempel på level curve översättning i meningar, lyssna på uttal och lära dig grammatik29 Exact Equations and Level Curves 151 29 Exact Equations and Level Curves A level curve or a conservation law is an equation of the form U(x;y) = c Hikers like to think of Uas the altitude at position (x;y) on the map and U(x;y) = cas the curve which represents the easiest walking path, that is, altitude does not change along that routeLevel curves The graph of a function f(x,y) can be studied by drawing level curves f(x,y)=c corresponding to various values of the constant c There is a Maple command that will plot several level curves in the same plot for a given function with evenly spaced values of c




Level Curves



Gradients And Level Curves
Level curves are obtained by setting f equal to a constant In the case of a circle for example f(x,y) = x^2 y^2 9 if I set f(x,y) = k where 9 < kLevel Curves and Cross Sections Main Concept A level curve of the surface is a twodimensional curve with the equation , where k is a constant in the range of f A level curve can be described as the intersection of the horizontal plane with the surfaceLevel curves A level curve is just a 2D plot of the curve f ( x, y ) = k, for some constant value k Thus by plotting a series of these we can get a 2D picture of what the threedimensional surface looks like In the following, we demonstrate this This is essentially an animation that you can go through step by step




Level Sets Math Insight




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
Level curveの意味や使い方 水準線,等位線 約1174万語ある英和辞典・和英辞典。発音・イディオムも分かる英語辞書。The graph itself is drawn in an ( x, y, z) coordinate system Remark 2 Level curves of the same function with different values cannot intersect Remark 3 Level curves of utility functions are called indifference curvesThe increment for \ (\Delta u\) The default is 1 part in 1,000, which should often provide enough smoothness for many copulas in practice;



Applied Sciences Free Full Text Heuristic And Numerical Geometrical Methods For Estimating The Elevation And Slope At Points Using Level Curves Application For Embankments




Level Set Examples Math Insight
So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming fromA level curve of a function is also defined as the curve of points where the function has constant values In the simple sense, the level curve is simply a cross section of graph of function which when equated to some constant values for example a function of two variables the values taken as x and y, then level curve is the curve of points (x, y)But they won't be the level curves of a function for which this is the gradient 但 它们 不一定 是,某个 以该 向量 场 为 梯度 的 函数 的等值线。 open163com To model the ground with the correct heights we used the level curves drawn in the reference drawing 为了给 地面 模型 设置 合适 的 高




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube
A level curve of f ( x, y) is a curve on the domain that satisfies f ( x, y) = k It can be viewed as the intersection of the surface z = f ( x, y) and the horizontal plane z = k projected onto the domain The following diagrams shows how the level curves f ( x, y) = 1 1 − x 2 − y 2 = k changes as k changesLevel curves Level Curves For a general function z = f ( x, y), slicing horizontally is a particularly important idea Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = cLevel curves level curves Log InorSign Up x 2 y 2 − z 2 = 1 1 z =




Level Curves Of The Error Function Download Scientific Diagram




Level Curves And Implicit Differentiation Studocu
A level curve is simply a cross section of the graph of z=f(x,y) taken at a constant value, say z=c A function has many level curves, as one obtains a different level curve for each value of c in the range of f(x,y) Level curves The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of , the level curves of and intersect each other at right anglesWe will now look at another definition is applying these level curves Definition Let be a two variable realvalued function Then the projection of the set of level curves of onto the plane is called the Contour Plot or Contour Map of When we depict a contour plot of a two variable function, it is important to note that it is impossibly to
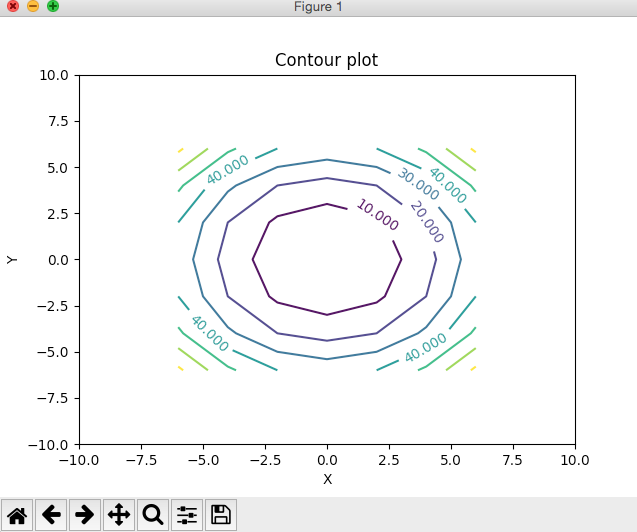



Contour Plot Using Python And Matplotlib Pythontic Com
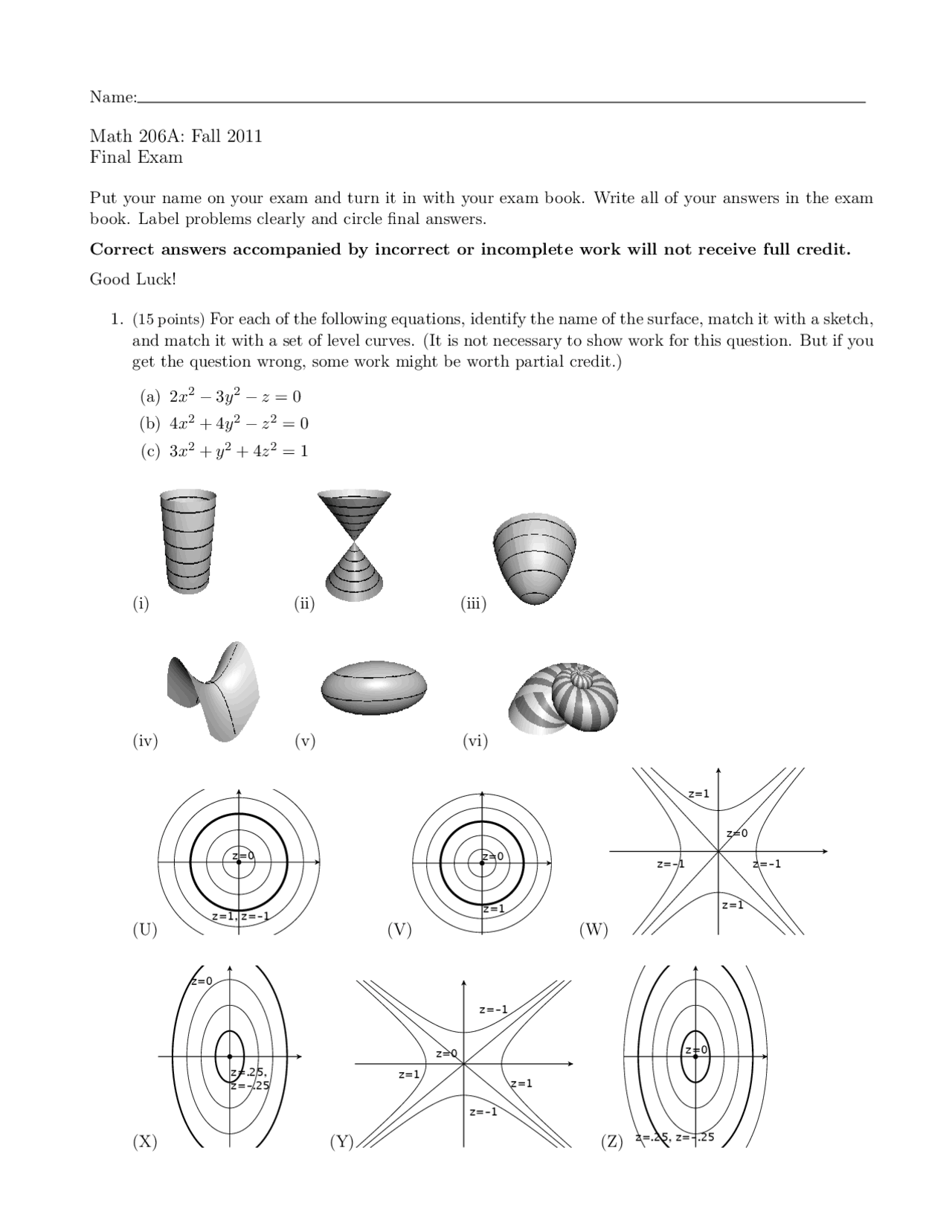



Level Curves Multivariable Exam Docsity
Download Wolfram Player Let be a realvalued function of two real variables and let be a constant The set of all points (, ) in the plane such that is called a level curve of (with value ) Contributed by Osman Tuna Gökgöz (March 11)Level Curves In mathematics, a level set of a realvalued function f of n real variables is a set where the function takes on a given constant value c1 In your first example, the proper solution is y = ± k − x 2 You left out the plusorminus That is not a small thing there are usually two values of y for each x, and that greatly affects the plotting of the curves I would say that there is no single general method for finding level curves, in a similar way that there is no general



Contour Lines Rodolphe Vaillant S Homepage



1
Level Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of cFor a general function z = f ( x, y), slicing horizontally is a particularly important idea Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve




Level Curves Of C R R Solid Lines Limiting Curve Labeled Zero Download Scientific Diagram




Level Sets Math Insight




Some Level Curves For The Total Energy E U V The Trajectory That Download Scientific Diagram
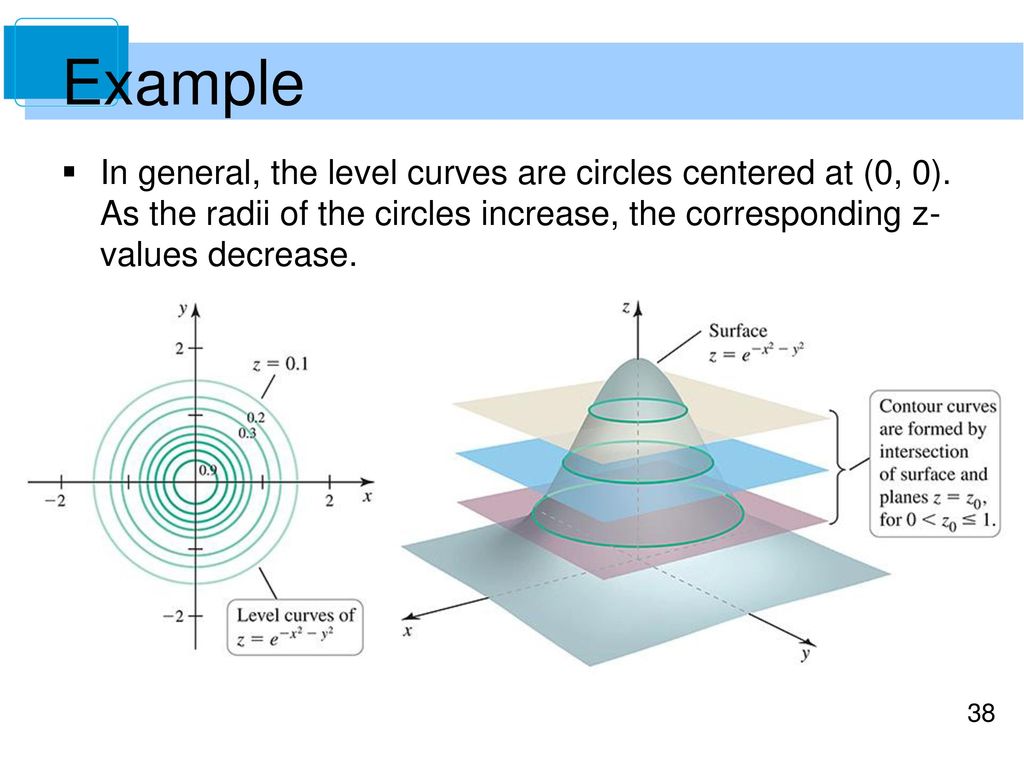



Introduction To Functions Of Several Variables Ppt Download



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf




Surface From Level Curves Of Unkown Levels In Matlab Stack Overflow




2 4 Pts Which Of The Following Are The Level Curve Graphs For F X Y Et Y Homeworklib




Describe The Level Curves Of The Function Z X2 Chegg Com




Relation Between Level Curves And Horizontal Traces Tex Latex Stack Exchange




Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F Xy Study Com
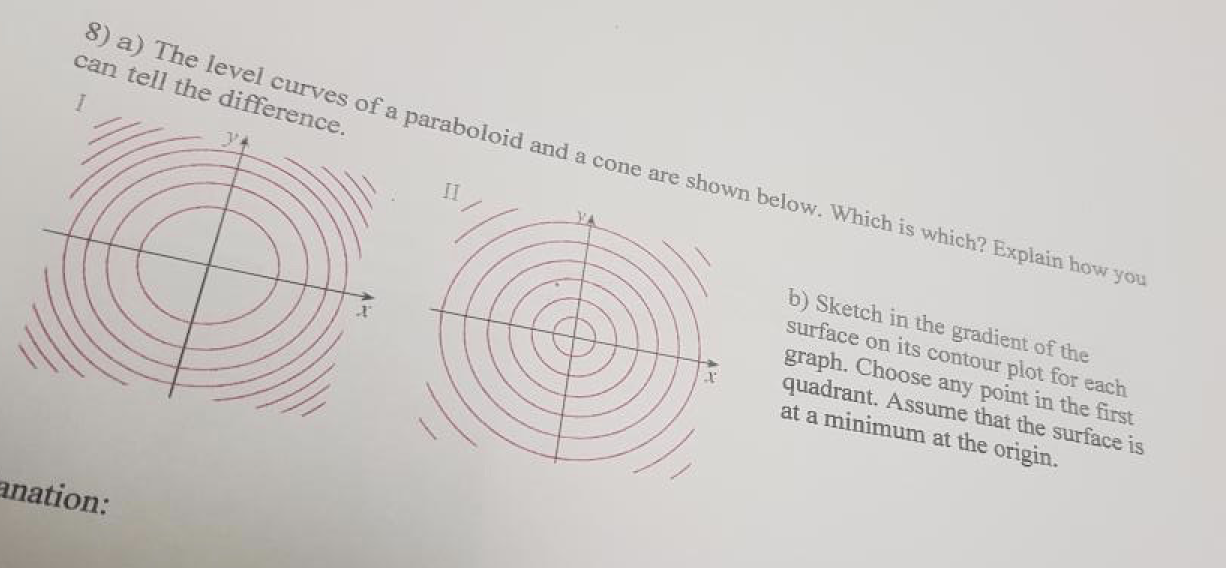



8 A The Level Curves Of A Paraboloid And A Cone Are Chegg Com
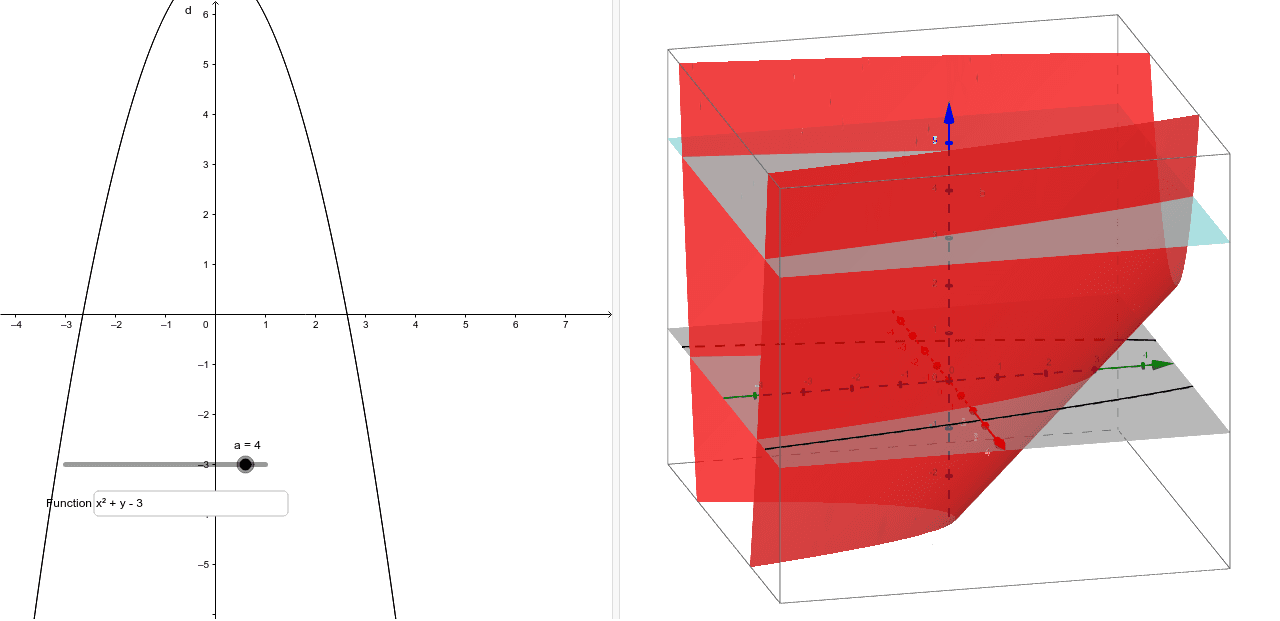



Visualizing Level Curves Geogebra




Level Curves High Res Stock Images Shutterstock




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
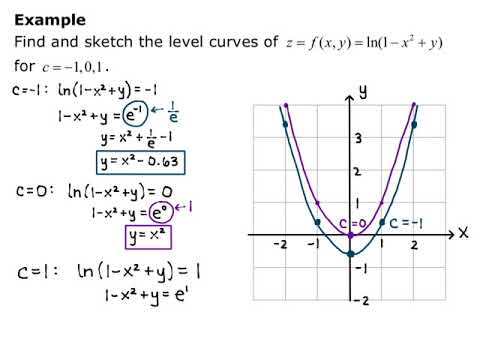



Section 13 1 Level Curves Youtube




Calculus Iii Functions Of Several Variables



Relief Functions And Level Curves



Level Curves And Contour Plots Mathonline




Level Sets Ximera
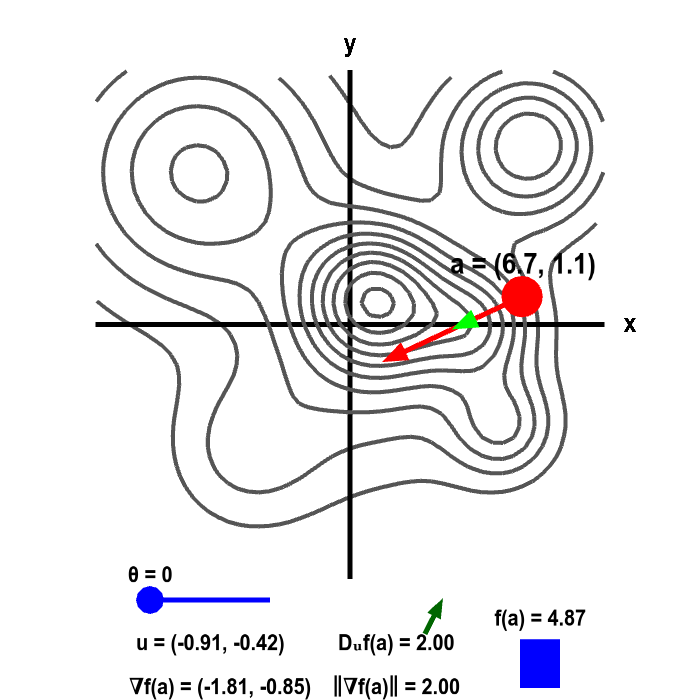



Applet Gradient And Directional Derivative On A Mountain Shown As Level Curves Math Insight



1



Example Contour Plots Or Level Curves



Rpubs Com Prashantd




Calculus Iii Functions Of Several Variables
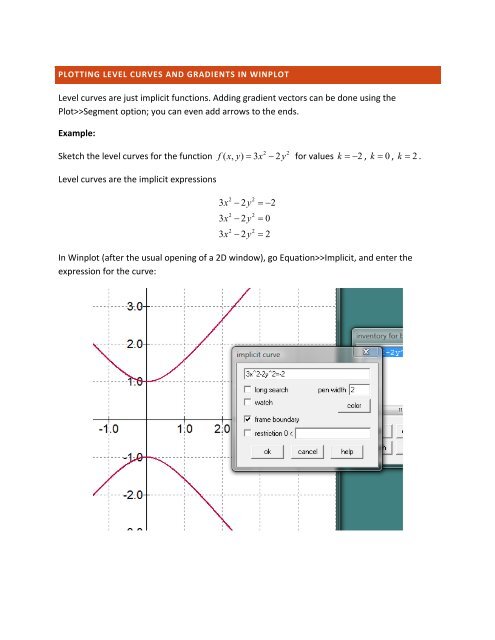



Level Curves And Gradient Vectors In Winplot




Schematic Level Curves Of G P Q Values Of Wbow Kernel And The New Download Scientific Diagram



The Level Curves Of X R 2 X 2 P T E T X X 0 2 2 For Download Scientific Diagram




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow




How To Sketch Level Curves Youtube



A Use A Cas And The Concept Of Level Curves To Plot Representative Graphs Of Members Of The



Sketch The Level Curves For The Following Functions And The Values 2 1 1 2 And Describe Sarthaks Econnect Largest Online Education Community



Level Curves In Autocad Download Cad Free 315 34 Kb Bibliocad
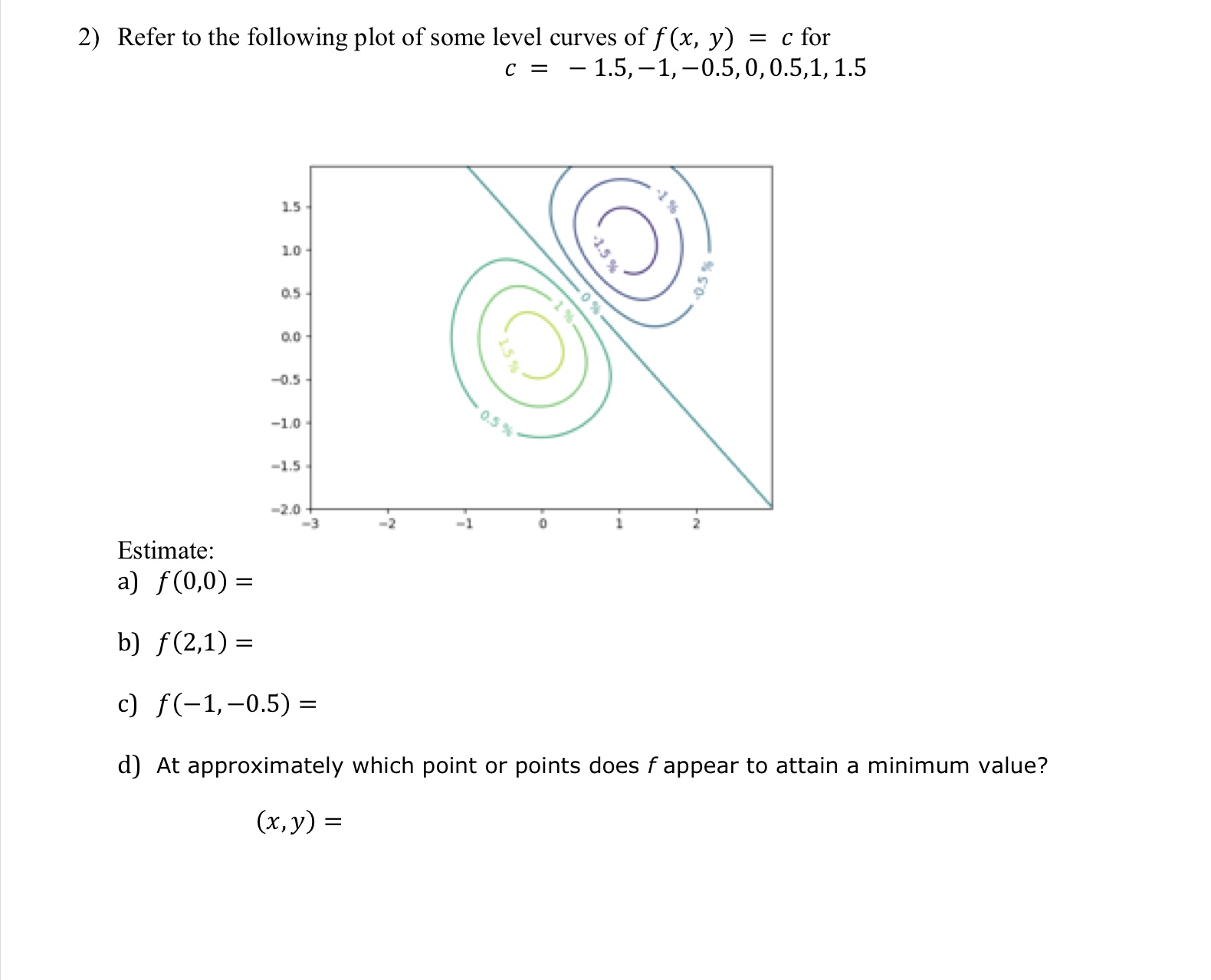



Answered Refer To The Following Plot Of Some Bartleby




Lesson 15 Gradients And Level Curves




Level Sets Math Insight



Level Curves



Relief Functions And Level Curves




Level Curves In Mathbb R 3 Mathematics Stack Exchange




Univ Vector Calculus Drawing A Contour Map With Level Curves Learnmath
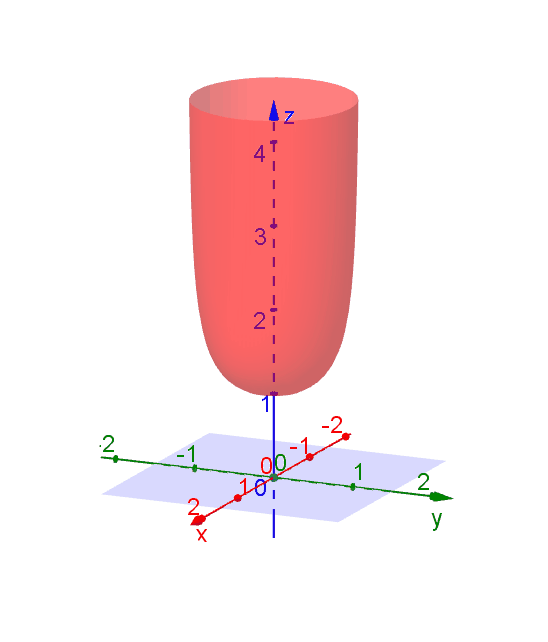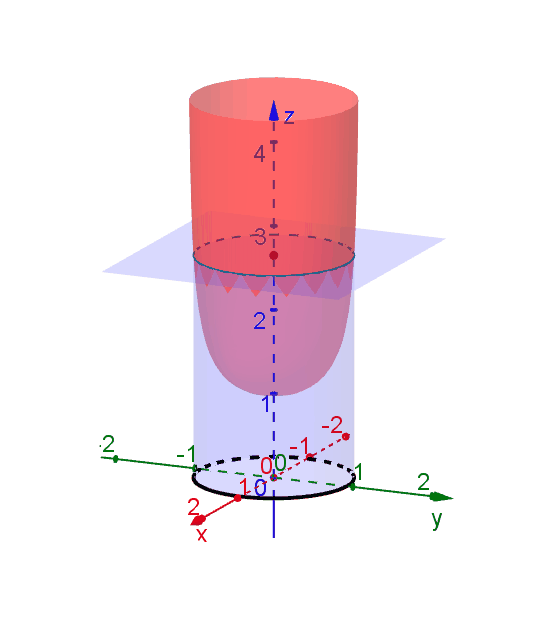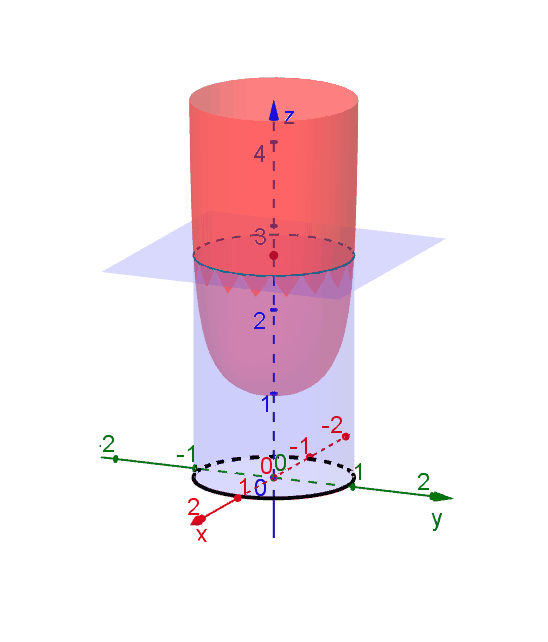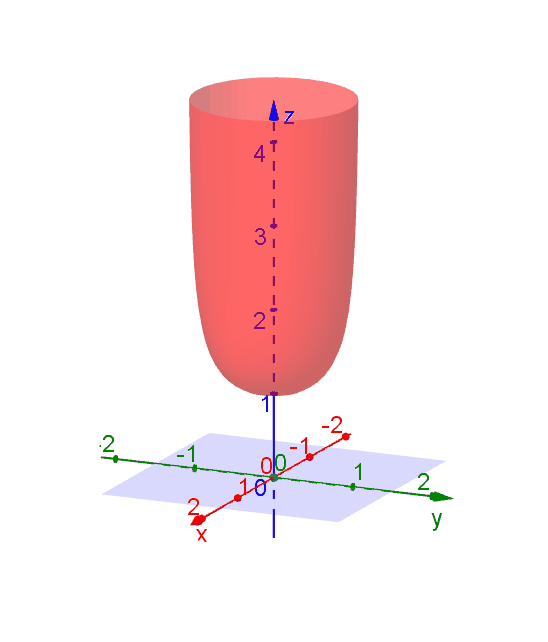



Level Curves Geogebra Dynamic Worksheet



Problem Of Level Curves Leading Lesson




Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com



Contour Lines Rodolphe Vaillant S Homepage




Gradient And Level Curve Geogebra




Describe The Level Curves Of The Function Sketch The Level Curves For The Given Values Of C F X Y X 2 2y 2 C 0 1 2 3 4 Study Com



Music Frequency Level Color Icon Vibration Noise Level Curves Sound Pink Waves Waveforms Digital Soundwaves Soundtrack Rhythm Abstract Geometri Stock Vector Image Art Alamy
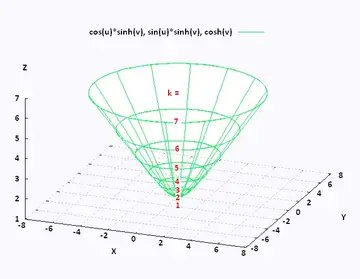



Mathematics Calculus Iii




Level Curves Calculus
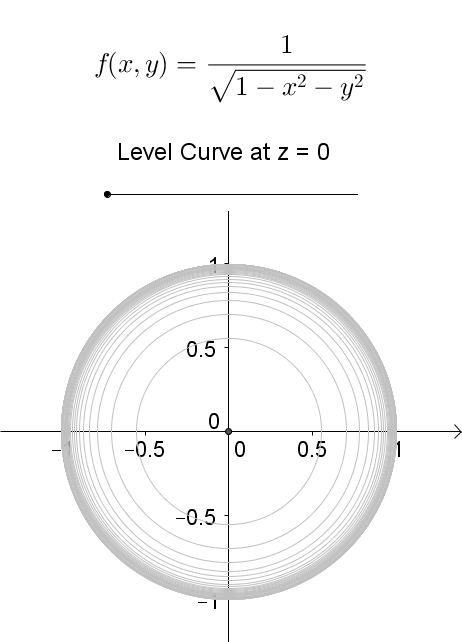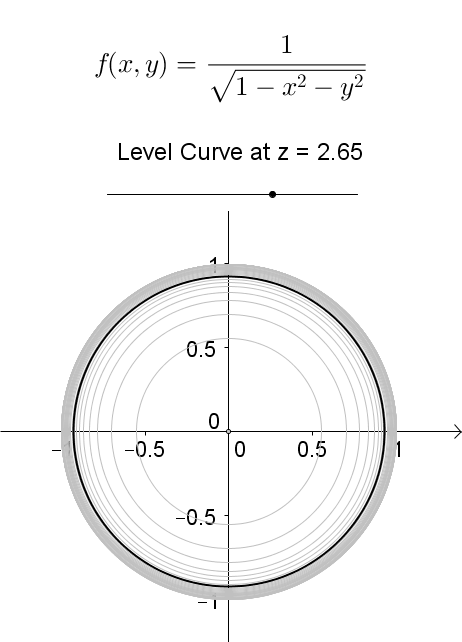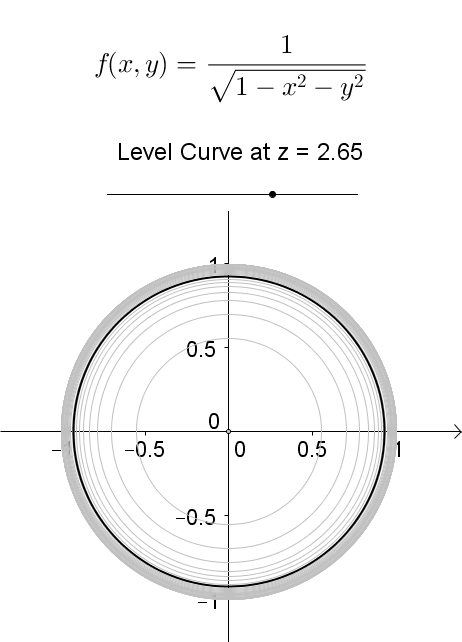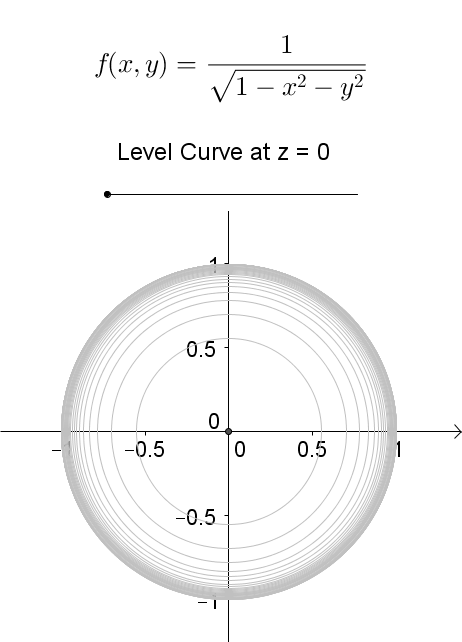



Level Curves Geogebra Dynamic Worksheet




Graphs And Level Curves




How Do You Plot Level Curves Describing A 3d Surface On The X Y Plane Mathematica Stack Exchange




Left Level Curves Of Distorted Density F X Y Center Level Download Scientific Diagram




Level Set Wikiwand



Level Curves Nb



Contour Map Of The Function Showing Several Level Curves Physics Forums
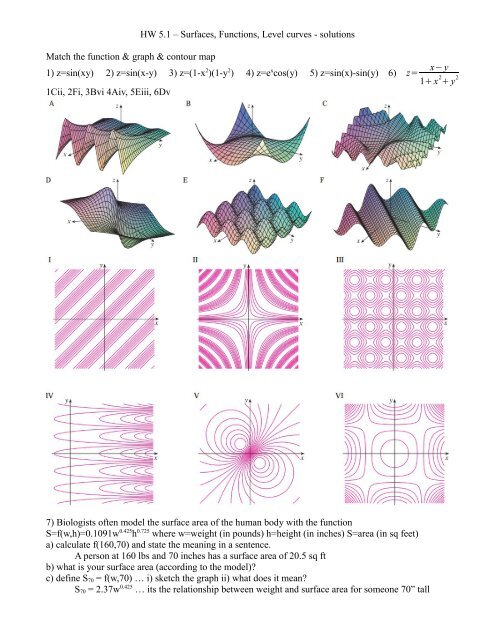



Hw 5 1 A Surfaces Functions Level Curves Solutions Match The




Level Curves Of Functions Of Two Variables Youtube
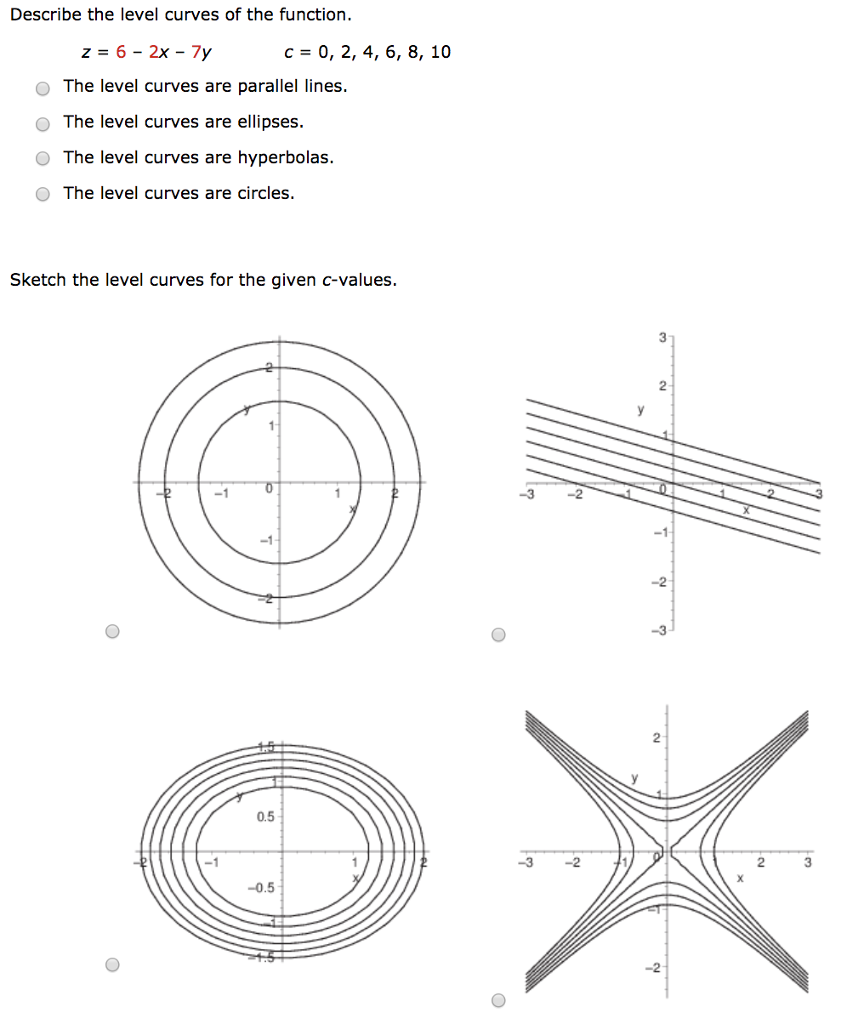



Describe The Level Curves Of The Function Z 6 2x 7y Chegg Com
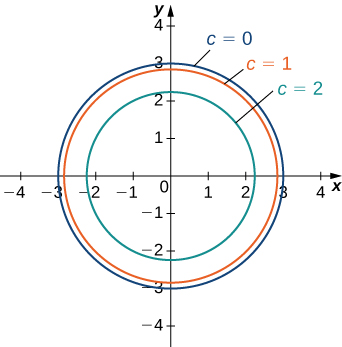



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize



Level Sets Ximera




Level Curves



1
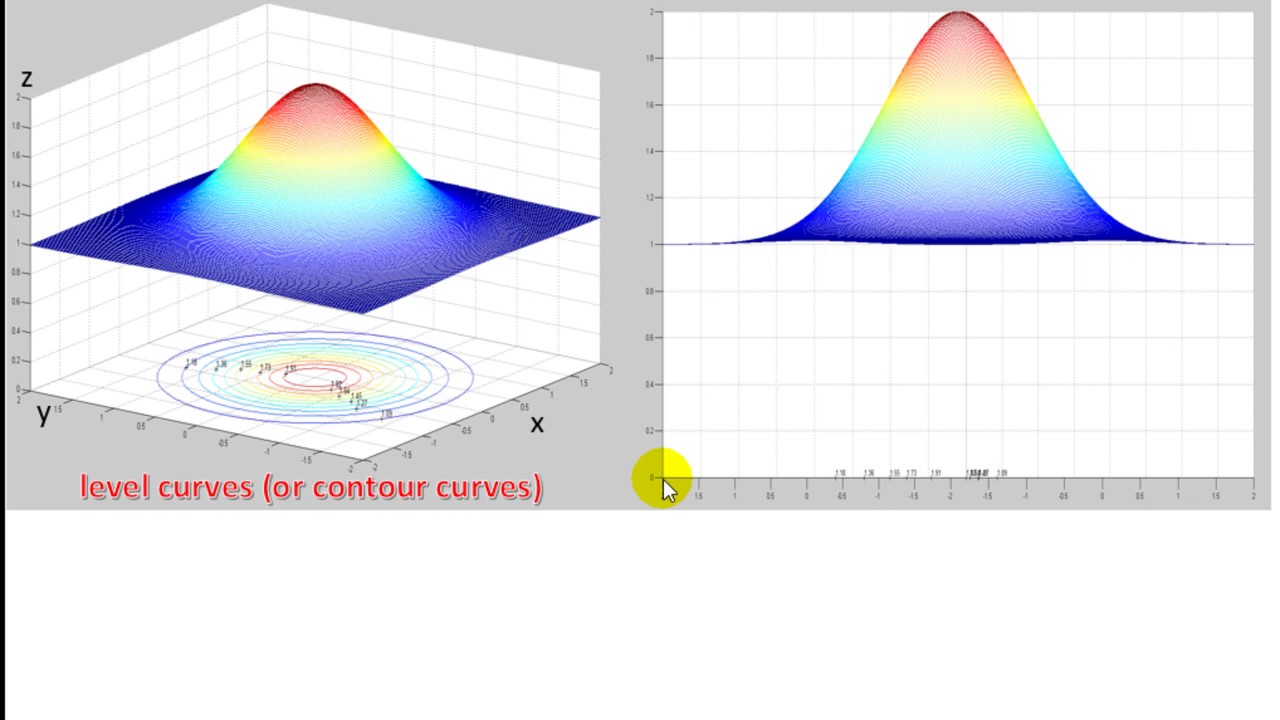



Level Curves Or Contour Curves Youtube




Level Set Wikipedia
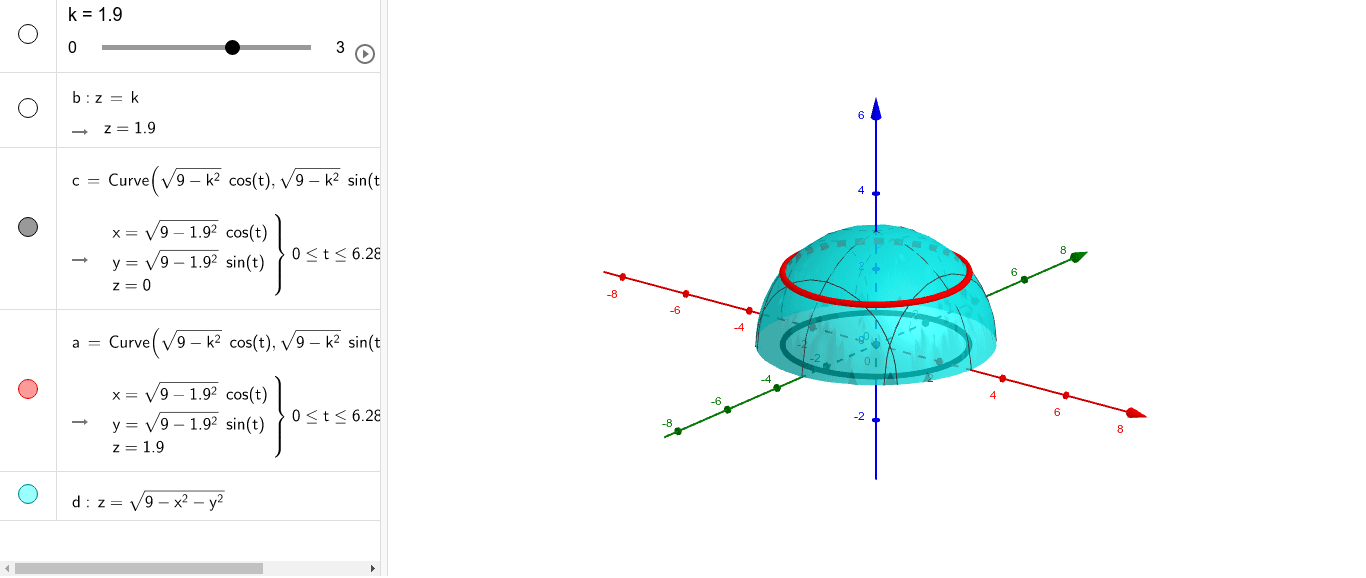



Sec 14 1 Level Curves And Surfaces Geogebra
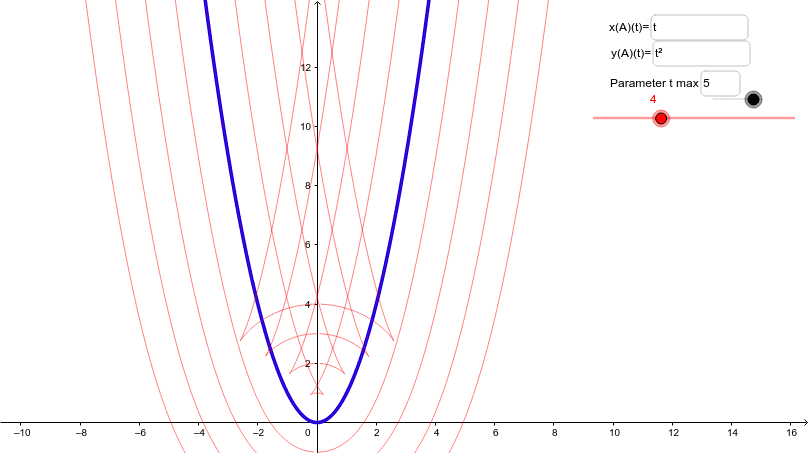



Level Curves Geogebra



Www3 Nd Edu Taylor Math550 Images Currentexamsolutions Exam2f16 Pdf




Level Curves
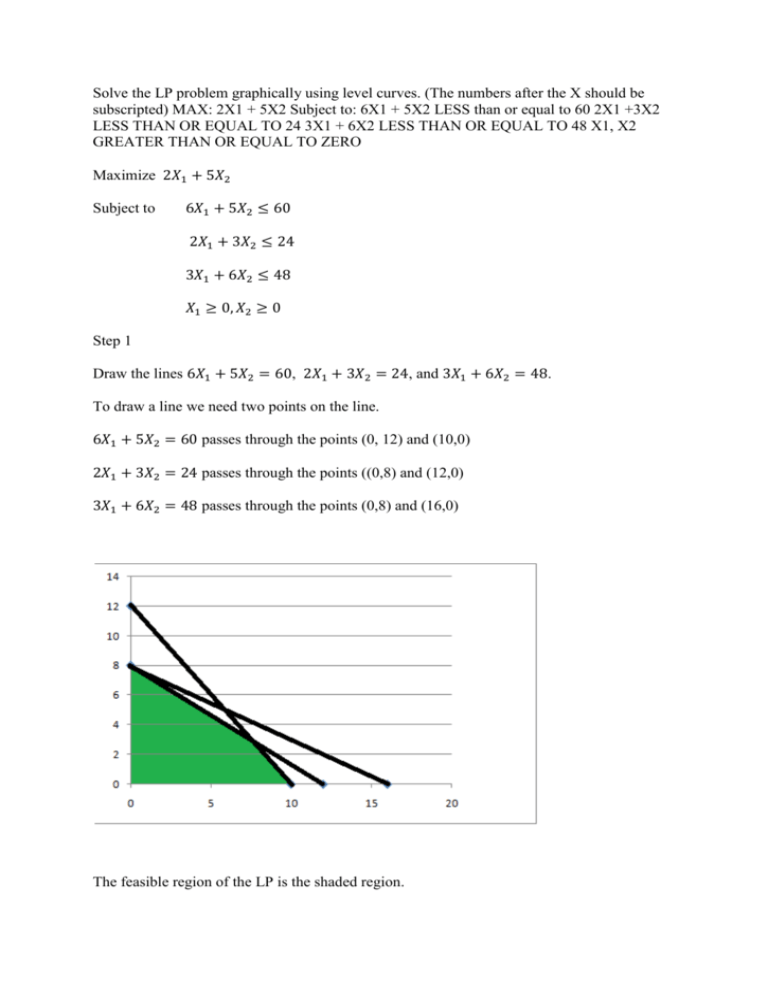



Solve The Lp Problem Graphically Using Level Curves The Numbers




Sketch The Level Curves Of The Function G X Y Chegg Com



1
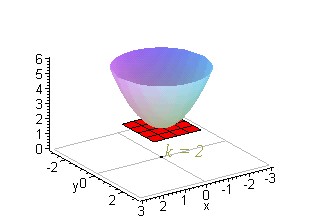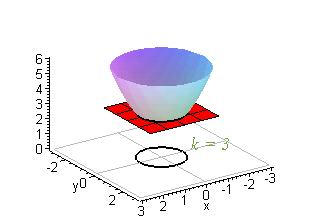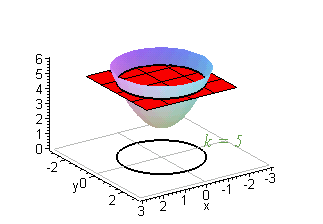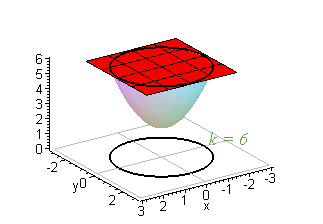



Gradients And Level Curves
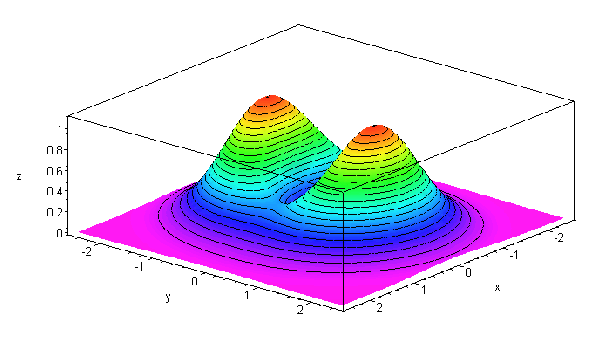



Level Curves




Problems With Level Curves First Steps Julialang
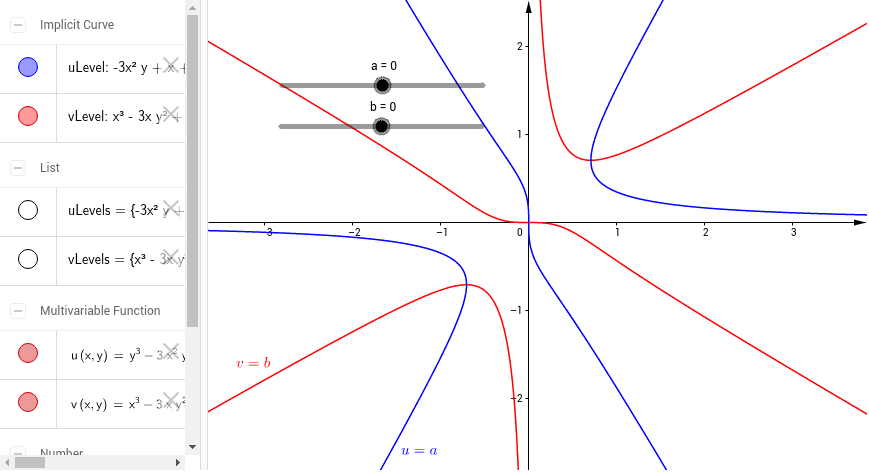



Level Curves Geogebra
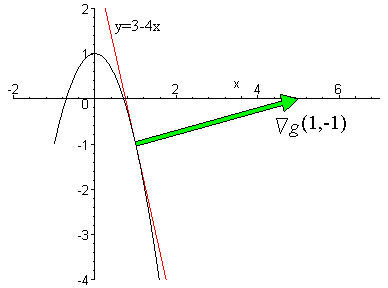



Gradients And Level Curves




Level Curve And A Surface Tex Latex Stack Exchange




Level Curves Example 1



Http Academic Brcc Edu Ryanl Modules Multivariable Traces Traces Pdf




Visualizing Surface And Level Curves Youtube



0 件のコメント:
コメントを投稿