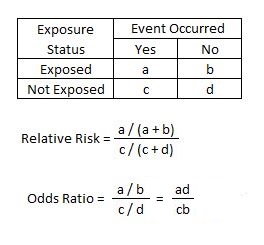
· The risk ratio (RR), also called the relative risk, is the ratio of the probability of cancer in smokers to the probability of cancer in nonsmokers RR = (a/ (ab))/ (c/ (cd)) = (a (cd))/ (c (ab)) Given that you know a, b, c, and d, you can compute either of these metricsAlso I have difficulty understanding different study designs and ends up misinterpreting them Is there an easier way of understanding the difference between cohort studies, case control studys, retrospective cohort studies and crosssectional studiesThis implausible scenario is shown in Table 5, where collapsed counts for low (or high) risk subjects only produce a 2 × 2 table with an odds ratios of 400

Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
What is the difference between odds ratio and relative risk
What is the difference between odds ratio and relative risk- · Odds ratio vs relative risk Odds ratios and relative risks are interpreted in much the same way and if and are much less than and then the odds ratio will be almost the same as the relative risk In some sense the relative risk is a more intuitive measure of effect sizeThe relative risk and the odds ratio are measures of association between exposure status and disease outcome in a population Relative risk In epidemiology, relative risk (RR) can give us insights in how much more likely an exposed group is to develop a certain disease in comparison to a nonexposed group



Table 1 From When To Use The Odds Ratio Or The Relative Risk Semantic Scholar
· If a 95% CI for the odds ratio does not include one, then the odds are said to be statistically significantly different We again reconsider the previous examples and produce estimates of odds ratios and compare these to our estimates of risk differences and relative risks ExampleThe literature dealing with the relation between relative risk and odds ratio is quite exten sive (some examples are (Davies et al, 1998; · Examples of measures of association include risk ratio (relative risk), rate ratio, odds ratio, and proportionate mortality ratio Risk ratio Definition of risk ratio A risk ratio (RR), also called relative risk, compares the risk of a health event (disease, injury, risk factor, or death) among one group with the risk among another group
Zhang and Yu, 1998))260 · Risk ratios, odds ratios, and hazard ratios are three common, but often misused, statistical measures in clinical research In this paper, the authors dissect what each of these terms define, and provide examples from the medical literature to illustrate each of these statistical measures Finally, the correct and incorrect methods to use these measures are summarizedThe above sample size calculator provides you with the recommended number of samples required to estimate the true odds ratio with the required relative precision and confidence level Try changing the five inputs (the relative precision, confidence level, absence case prevalence, expected odds ratio and presence to absence ratio) to see how they affect the sample size
In clinical studies, as well as in some other settings, the parameter of greatest interest is often the relative risk rather than the odds ratio The relative risk is best estimated using a population sample, but if the rare disease assumption holds, the odds ratio is a good approximation to the relative risk — the odds is p / (1 − p), so when p moves towards zero, 1 − p moves towards 1, meaning that the odds approaches the risk, and the odds ratio approaches the relative riskThis video will show you how to calculate and interpret odds ratios and risk ratios with an exampleFor more assistance with statistics, consider this bookMFor example, a risk ratio of 075 translates to a relative risk reduction of 25%, as in the example above The risk difference is often referred to as the absolute risk reduction (ARR), and may be presented as a percentage (for example, 1%), as a decimal (for example, 001), or as counts (for example, 10 out of 1000)


Relative Risk Odds Ratio



How To Calculate Relative Risk And Odds Ratio Google Search
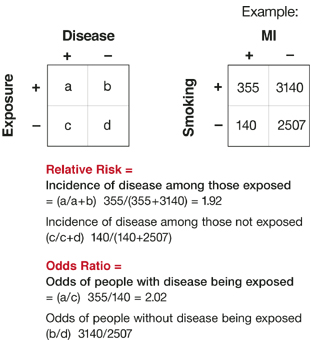
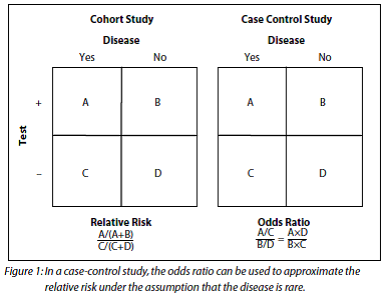
The more common the disease, the larger is the gap between odds ratio and relative risk In our example above, p wine and p no_wine were 0009 and 0012 respectively, so the odds ratio was a good approximation of the relative risk OR = 0752 and RR = 075 If the risks were 08 and 09, the odds ratio and relative risk will be 2 very different numbers OR = 044 and RR = 0 Relative · Definition The Odds Ratio is a measure of association which compares the odds of disease of those exposed to the odds of disease those unexposed Formulae OR = (odds of disease in exposed) / (odds of disease in the nonexposed) Example I often think food poisoning is a good scenario to consider when interpretting ORs Imagine a group of friends went out toWhen prevalence of the event is low, the odds ratio provides a good estimate of the relative risk (Agresti 02) In this situation, the odds ratio estimates from PROC FREQ or the usual logistic model (the default logitlinked, binomial model) fit by PROC LOGISTIC can be used to



Relative And Atribute Risk



Odds Ratio Article
Relative Risk and Odds Ratio for the obese 3) Overall, you can see that decreasing the baseline incidence will decrease the odds ratio (300 in those who are nonobese versus 129 in those who are obese) Obviously, these results run counter to expected results, putting the onus on the researcher to justify them Similarly, you should findThe odds ratio supports clinical decisions by providing information on the odds of a particular outcome relative to the odds of another outcome In the endocarditis example, the risk (or odds) of dying if treated with the new drug is relative to the risk (odds) of dying if treated with the standard treatment antibiotic protocol · The basic difference is that the odds ratio is a ratio of two odds (yep, it's that obvious) whereas the relative risk is a ratio of two probabilities (The relative risk is also called the risk ratio) Let's look at an example Relative Risk/Risk Ratio Suppose you have a school that wants to test out a new tutoring program


Summarising Binary Data Health Knowledge


Relative Risk Odds Ratio
· a relative risk ratio is one probability divided by another;Or population of interest The relative risk (RR) is the risk of the event in an experimental group relative to that in a control group The odds ratio (OR) is the odds of an event in an experimental group relative to that in a control group An RR or OR ofSample size requirements for studies estimating odds ratios or relative risks This paper presents formulae for determining the number of subjects necessary, in either a casecontrol or a cohort study, to estimate the odds ratio or relative risk, respectively, to within a selected percentage (epsilon) of the true population value with some



Measures Of Association Ppt Download



Cph Exam Review Epidemiology Ppt Download
· Relative risk is the ratio of the risk faced by one group to the risk faced by another group This can be used to express the risk of a state, behavior or strategy as compared to a baseline riskOdds Ratio (OR) is a measure of association between exposure and an outcome (RR = Relative Risk) The reason is that a casecontrol study begins from outcome ie selection of a sample with the outcome of interest which in this case is endometrial cancer · Rate ratios are closely related to risk ratios, but they are computed as the ratio of the incidence rate in an exposed group divided by the incidence rate in an unexposed (or less exposed) comparison group Consider an example from The Nurses' Health Study This prospective cohort study was used to investigate the effects of hormone replacement therapy (HRT) on coronary


How To Interpret The Odd Ratio And P Value



What Is The Difference Between The Risk Ratio Rr And The Odds Ratio Or Quora
The quote surely just means to say that the odds ratio is a relative risk measure rather than an estimate of the relative risk, which as already point out is only approximately the case in cohort studies/randomized trials for very low proportions By relative risk measure I mean something that is given relative to some comparison group in a way that the absolute difference depends on8116 · Percent increase = (Risk Ratio lower bound – 1) x 100 Percent decrease = (1 – Risk Ratio upper bound) x 100 It's worth stating again when comparing two proportions close to 1 or 0, the risk ratio is usually a better summary than the raw difference Odds Ratios We now turn to odds ratios as yet another way to summarize a 2 x 2 tableThe simple relative risk is 055 and the simple odds ratio is 025Clearly the probability of fathering a child is strongly dependent on a variety of demographic variables, especially age (the issue of marital status was dealt with by a separate analysis) The control group was 84 years older on average (435 years versus 351), showing the need to adjust for this variable



3 Data For Example 7 3 To Illustrate The Need For The Disease To Be Download Table


Frontiers Odds Ratio Or Prevalence Ratio An Overview Of Reported Statistical Methods And Appropriateness Of Interpretations In Cross Sectional Studies With Dichotomous Outcomes In Veterinary Medicine Veterinary Science
4509 · The odds ratio will estimate the average change in odds (the average odds ratio) among exposed individuals only when all individual odds ratios are equal and all individual outcome risks without exposure are equal 1;2ERA–EDTA Registry, Department of Medical Informatics, Academic Medical Center, UniversityThis is not true for relative risk Switching the rows or columns inverts the odds ratio For example, the odds ratio for no cough given a history of bronchitis = (247/26)/(1002/44) = 0417 = 1/2397 This is the reciprocal of the OR for cough There are only two possible odds ratios, as switching both rows and columns gives


Introduction To Genetic Epidemiology Lesson 5 Analyzing The Data


Introduction To Genetic Epidemiology Lesson 5 Analyzing The Data
29 · A risk or odds ratio = 1 indicates no difference between the groups A risk or odds ratio > 1 indicates a heightened probability of the outcome in the treatment group The two metrics track each other, but are not equal An example with a control group and a therapy treatment group Treatment group 5 deaths, 95 survive Risk = 5/100 = 0057214 · The odds ratio will be greater than the relative risk if the relative risk is greater than one and less than the relative risk otherwise In the example above, if the adjusted odds ratio were interpreted as a relative risk, it would suggest that the risk of antibiotic associated diarrhoea is reduced by 75% for the intervention relative to the placebo group6410 · RELATIVE RISK AND ODDS RATIO Risk and Odds just seemed the same to me for a long time Since then, I have come to understand to important difference Lets start with Relative Risk Relative Risk can be addressed by asking the following question How many times more likely is an "exposed" group to develop a



Relative Risk And Odds Ratios Examples


A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence
· Is Odds ratio the same as relative risk ratio?About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators7014 · For example, the odds of suffering a heart attack in smokers is calculated dividing the likelihood of having an attack in smokers (infarcted smokers divided by the total number of smokers, same that we did with the risk) by the probability of not suffering the attack in smokers (noninfarcted smokers divided by the total number of smokers or, equivalently, one minus the


Confluence Mobile Wiki Ucsf



Using Odds Ratio In Case Control Studies Youtube
Measures of effect Relative risks, odds ratios, risk difference, and 'number needed to treat' G Tripepi1, KJ Jager2, FW Dekker2,3, C Wanner4 and C Zoccali1 1CNRIBIM, Clinical Epidemiology and Physiopathology of Renal Diseases and Hypertension of Reggio Calabria, Reggio Calabria, Italy; · Relative measures of effect are risk ratio (ie the ratio between two incidence proportions), incidence rate ratio (the ratio between two incidence rates), and OR (the ratio between two odds) The risk difference is an absolute measure of effect (ie the risk of the outcome in exposed individuals minus the risk of the same outcome in unexposed) · A lot of confusion would be saved (in my view) if we could call these "probability ratios" instead, but the term "relative risk ratio" seems to be here to stay an odds ratio is one set of odds divided by another;
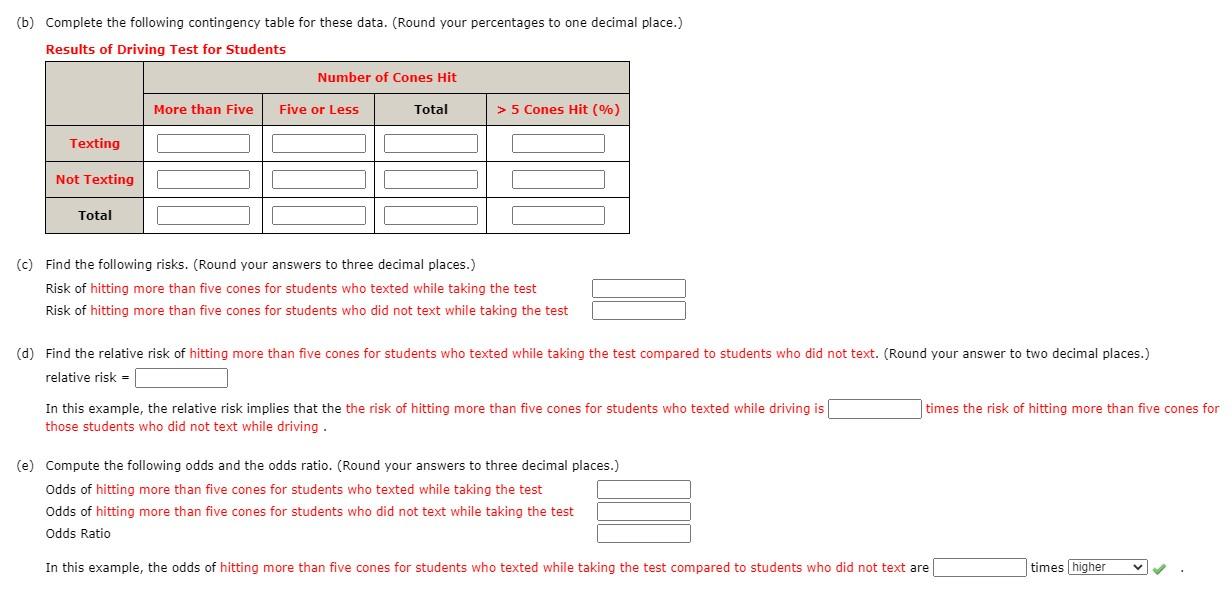


Solved Contingency Table And Risk Relative Risk Odds A Chegg Com



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
· What could be said is that the odds of failure is 374 times greater Risk Ratio vs Odds Ratio Whereas RR can be interpreted in a straightforward way, OR can not A RR of 3 means the risk of an outcome is increased threefold A RR of 05 means the risk is cut in halfFor example the probability of a tiger being diseased, divided by the probability of a bear being diseased A lot of confusion would be saved (in my view) if we could call these "probability ratios" instead, but the term "relative risk ratio" seems to be here to stay · Odds ratios are a common measure of the size of an effect and may be reported in casecontrol studies, cohort studies, or clinical trials Increasingly, they are also used to report the findings from systematic reviews and metaanalyses Odds ratios are hard to comprehend directly and are usually interpreted as being equivalent to the relative risk



Measures Of Effect Relative Risks Odds Ratios Risk Difference And Number Needed To Treat Sciencedirect



Odds Ratio Wikipedia
The risk ratio (or relative risk) is the ratio of the risk of an event in the two groups, whereas the odds ratio is the ratio of the odds of an event (see Box 92a) For both measures a value of 1 indicates that the estimated effects are the same for both interventionsRelative Risk (RR) & Odds Ratio (OR) The difference between odds and probability is important because Relative Risk is calculated with probability and Odds Ratio is calculated with odds Relative Risk (RR) is a ratio of probabilities or put another way it is one probability divided by another Odds Ratio (OR) is a ratio or proportion of oddsRelative risk is a ratio of the probability of an event occurring in the exposed group versus the probability of the event occurring in the nonexposed group For example, the relative risk of developing lung cancer (event) in smokers (exposed group) versus nonsmokers (nonexposed group) would be the probability of developing lung cancer for smokers divided by the probability


Absolute Risk Vs Relative Risk Vs Odds Ratio Pp Made Easy In Population Perspective Made Easy On Vimeo



What Is An Odds Ratio And How Do I Interpret It Critical Appraisal
Pute either the odds ratio or the relative risk to answer this question The odds ratio compares the relative odds of death in each group For women, the odds were exactly 2 to 1 against dying (154/308 05) For men, the odds were almost 5 to 1 in favor of death (709/142 4993) The odds ratio is 9986 (4993/05) There is a 10fold greaterOdds ratios (OR) are commonly reported in the medical literature as the measure of association between exposure and outcome However, it is relative risk that people more intuitively understand as a measure of association Relative risk can be directly determined in a cohort study by calculating a rFor example, the odds of a tiger being diseased, divided by the odds of a bear being diseased



Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios
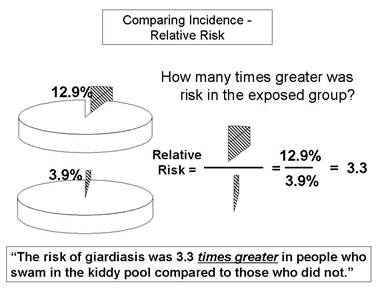


Relative Risk And Absolute Risk Definition And Examples Statistics How To
More on the Odds Ratio Ranges from 0 to infinity Tends to be skewed (ie not symmetric) "protective" odds ratios range from 0 to 1 "increased risk" odds ratios range from 1 to Example "Women are at 144 times the risk/chance of men" "Men are at 069 times the risk/chanceRelative Risk and Odds Ratios Examples Calculating Relative Risk Calculating Relative Risk Imagine that the incidence of gun violence is compared in two cities, one with relaxed gun laws (A), the other with strict gun laws (B) In the city with relaxed gun laws, there were 50 shootings in a



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
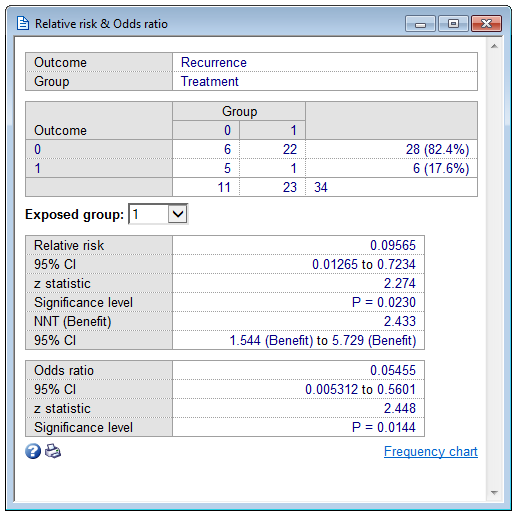


Relative Risk Odds Ratio



Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios



상대위험도 Relative Risk Vs 오즈비 Odds Ratio
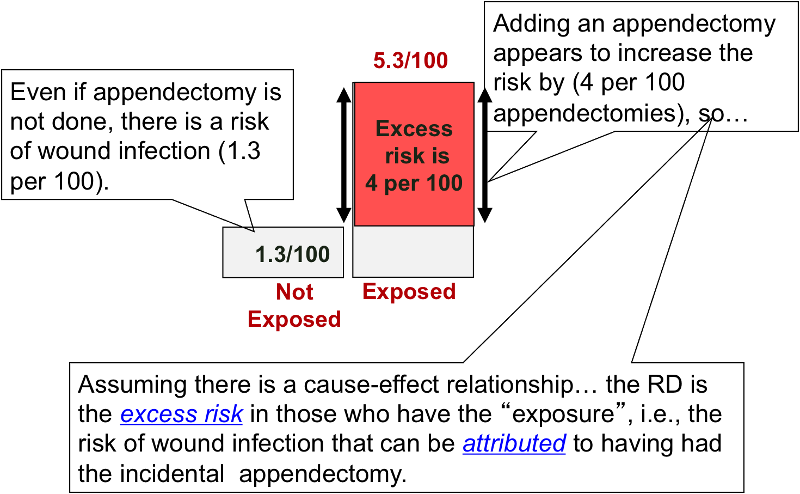


Risk Differences And Rate Differences



Odds Ratios The Odd One Out Stats By Slough



Reporting The Results Sage Research Methods



Estimating Risk



Converting An Odds Ratio To A Range Of Plausible Relative Risks For Better Communication Of Research Findings The Bmj



The Difference Between Relative Risk And Odds Ratios The Analysis Factor



Relative Risk Odds Ratios Youtube



How To Calculate Odds Ratio And Relative Risk In Excel Statology



Chapter 10 Chi Square Test Relative Risk Odds Ratios


Research Statistics Basics Contents 1 Basic Concepts 2 References Basic Concepts Null Hypothesis The Hypothesis That The Independent Variable Has No Effect On The Dependent Variable For Example Steroids Do Not Improve Outcomes In Ards Would Be


Relative Risk Article



Bar Graph Represents The Summary Odds Ratios Or Relative Risks Of The Download Scientific Diagram


Relative Risk Wikipedia



Solved Youll Need To Know Prevalence Rate Odds Rati Chegg Com



2x2 Table Homework The 2x2 Table Relative Risk And The Odds Ratio Jim Studocu


Relative Risks And Odds Ratios What S The Difference Mdedge Family Medicine


Introduction To Genetic Epidemiology Lesson 5 Analyzing The Data


How To Be Awesome At Biostatistics And Literature Evaluation Part Ii Tl Dr Pharmacy



Chapter 6 Choosing Effect Measures And Computing Estimates Of Effect Cochrane Training
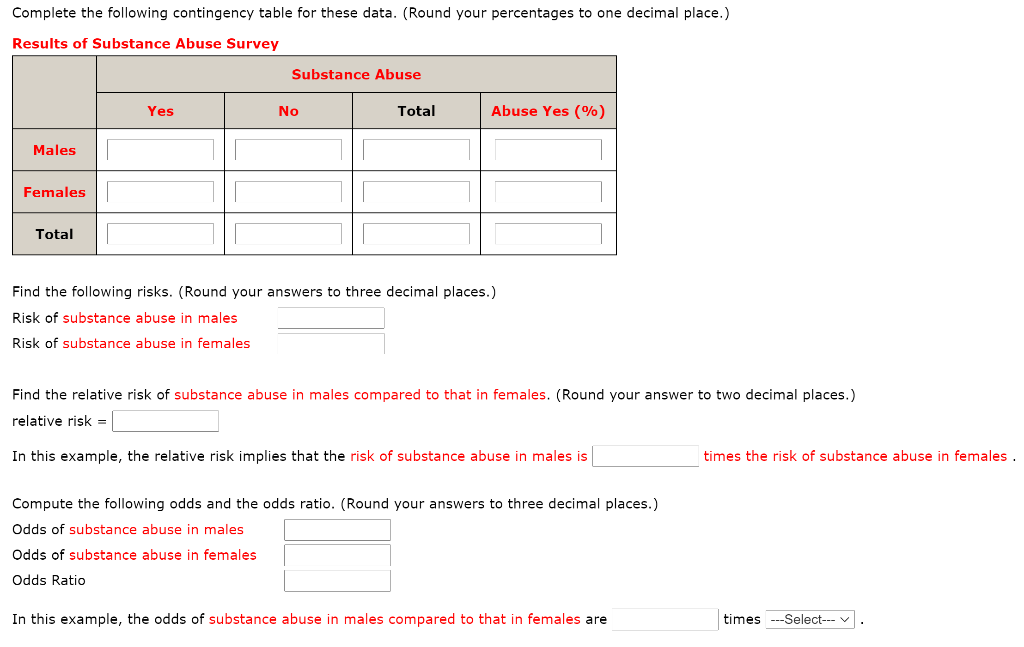


Solved Contingency Table And Risk Relative Risk Odds A Chegg Com



Common Measures Of Association In Medical Research Handout


A Beginner S Guide To Interpreting Odds Ratios Confidence Intervals And P Values Students 4 Best Evidence



What Is An Odds Ratio And How Do I Interpret It Critical Appraisal



Solved Present Example Of An Dolds Ratio Compared To A Re Chegg Com



How To Calculate Odds Ratio And Relative Risk In Excel Statology
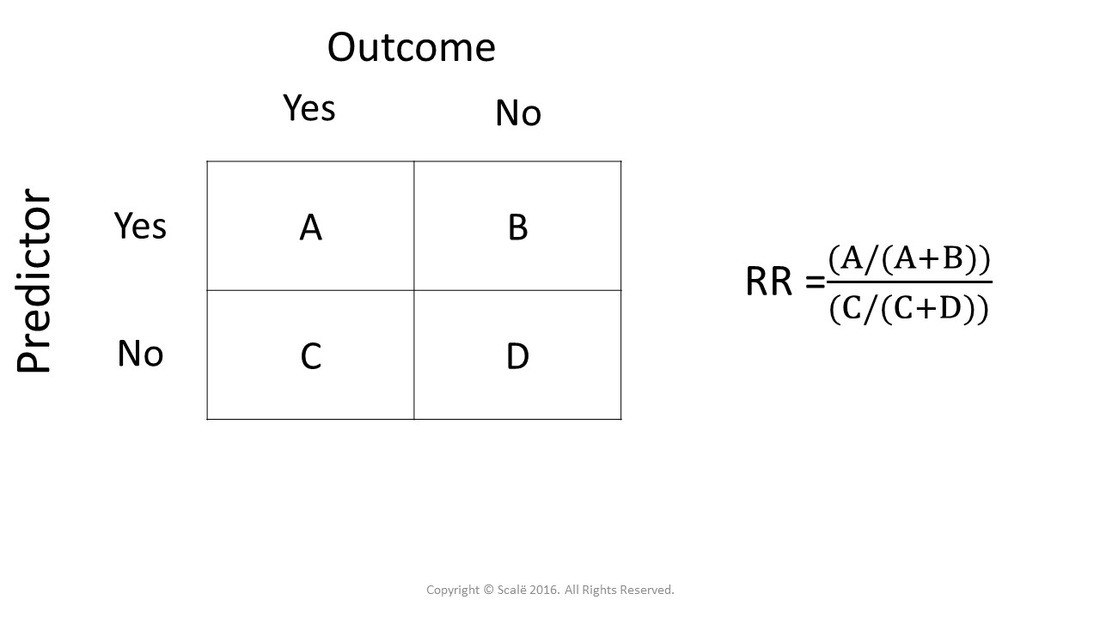


Calculate Relative Risk With 95 Confidence Intervals



What Does An Odds Ratio Or Relative Risk Mean



Odds Ratio Relative Risk Calculation Definition Probability Odds Youtube



Understanding Systematic Reviews And Meta Analysis Archives Of Disease In Childhood



When Can Odds Ratios Mislead The Bmj



Relative Risk Versus Odds Ratio Usmle Biostatistics 4 Youtube



How To Calculate Relative Risk 3 Steps With Pictures Wikihow



Relative And Atribute Risk



Relative Risk Wikipedia



Effect Sizes Basicmedical Key


Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1


Research Statistics Basics Contents 1 Basic Concepts 2 References Basic Concepts Null Hypothesis The Hypothesis That The Independent Variable Has No Effect On The Dependent Variable For Example Steroids Do Not Improve Outcomes In Ards Would Be



How To Calculate Odds Ratio And Relative Risk In Excel Statology



Table 1 From When To Use The Odds Ratio Or The Relative Risk Semantic Scholar



What Is The Difference Between The Risk Ratio Rr And The Odds Ratio Or Quora
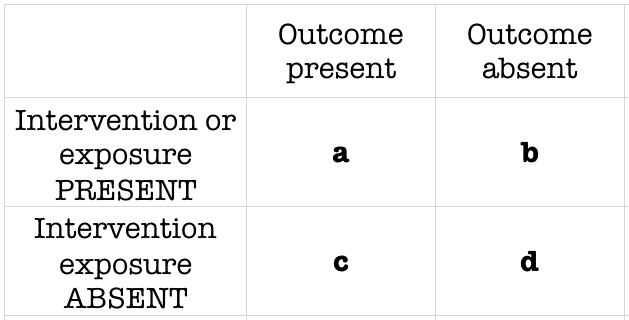


Odds Ratio Litfl Ccc Research
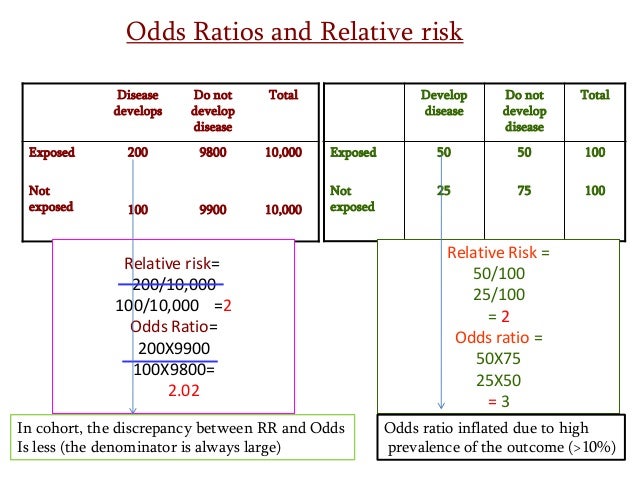


Estimating Risk



Odds Ratios And Risk Ratios Youtube


Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia


Understanding Absolute And Relative Risk In Medical Risk Analysis And Putting This In Context



Measuring Of Risk
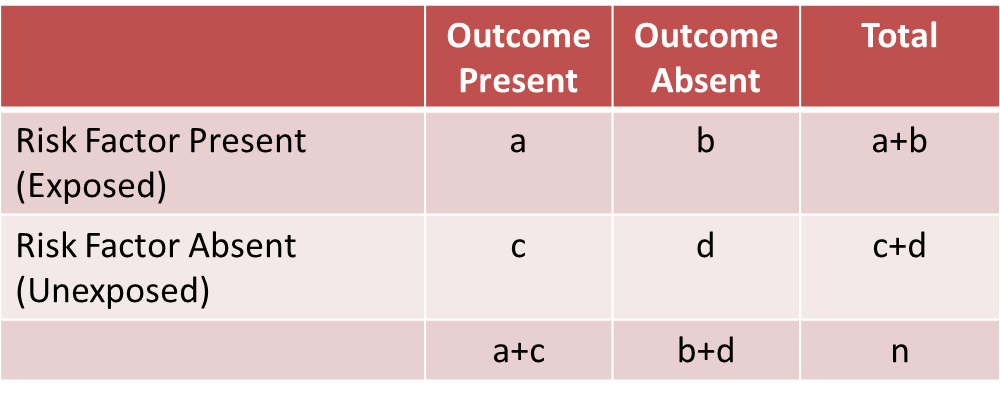


A Stratified Analysis


Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia


Icare An R Package To Build Validate And Apply Absolute Risk Models



What Does An Odds Ratio Or Relative Risk Mean


Risk Differences Odds Ratios And Relative Risks Plots With Proc Freq


Ctspedia Ctspedia Educationalmaterials018



Relative Risks Odds Ratios The Odds Ratio Two Binomials Coursera



Odds Ratio Wikipedia


Studying Studies Part I Relative Risk Vs Absolute Risk Peter Attia



Relative Risk Http Www Slideshare Net Terryshaneyfelt7 What Does An Odds Ratio Or Relative Risk Mean Study Skills Research Methods Study Tips
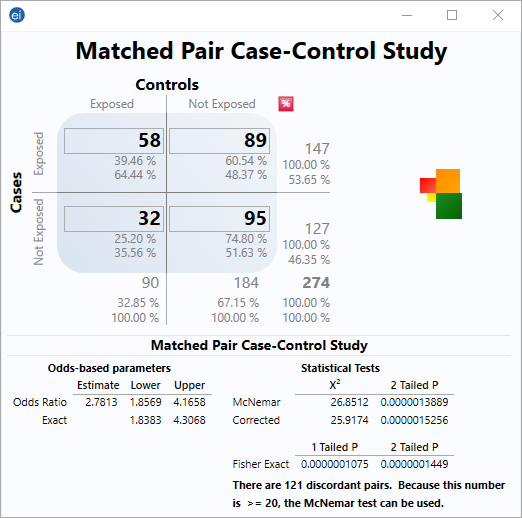


Matched Pair Case Control Statcalc User Guide Support Epi Info Cdc



Relative Risk Analysis And Odds Ratio Analysis
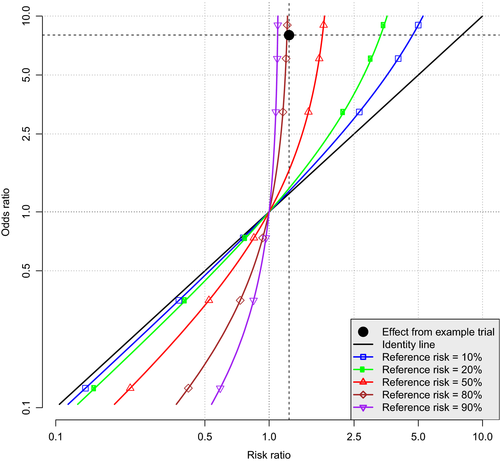


The Risks Of Odds Ratios Researcher An App For Academics



Relative Risk And Odds Ratio Usmle The Journey



Calculate Relative Risk With 95 Confidence Intervals


Relative Risk Ratios And Odds Ratios



How To Interpret And Use A Relative Risk And An Odds Ratio Youtube



Measures Of Effect Relative Risks Odds Ratios Risk Difference And Number Needed To Treat Sciencedirect



Statquest Odds Ratios And Log Odds Ratios Clearly Explained Youtube
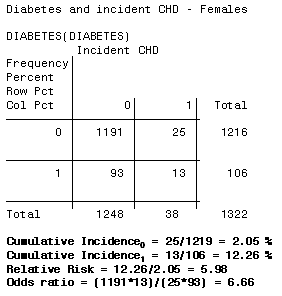


3 5 Bias Confounding And Effect Modification Stat 507



Solved Please Answer All Questions Parts Step By Step S Chegg Com
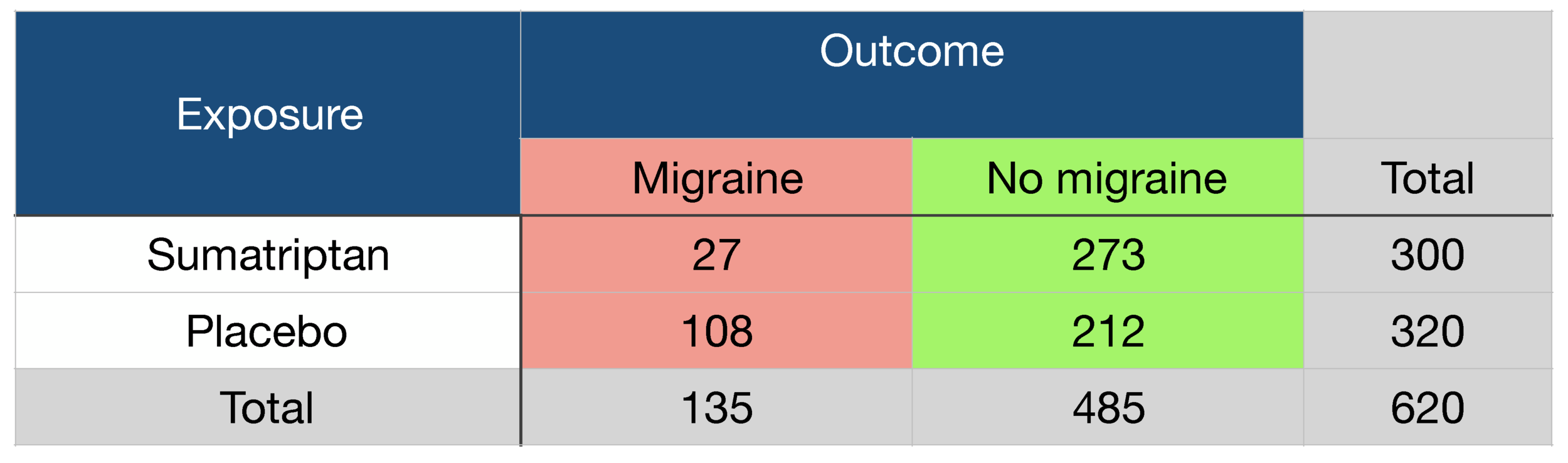


Probability Odds Ratio And Relative Risk Gp Raj



0 件のコメント:
コメントを投稿